本文面向有一定密码学基础，或者对密码学感兴趣的读者。文中虽有大量数学公式出现，但都比较简单不难理解。

导言：zkPoD 是什么？

zkPoD 实现了去中心化的「零知识有条件支付」，支持上 GB 数据的零信任公平交易。关于「零知识有条件支付」的概念请看这篇概述文章 『zkPoD：区块链，零知识证明与形式化验证，实现无中介、零信任的公平交易』。 zkPoD 是一个全新的实现 ZKCP 目标的方案。目前 zkPoD 已经支持上 GB 的数据，支持低 TPS 公链，也支持高 TPS 联盟链；既支持二进制数据，也支持带有内部丰富类型与结构的表格数据。与传统的「受信第三方」相比，zkPoD利用区块链来作为一个「Trustless 第三方」，实现「零信任公平交易」。

zkPoD 也是一个实现数据与价值双向流通的底层基础协议

zkPoD 开源代码与更多文档请见：https://github.com/sec-bit/zkPoD-node

Proof-of Delivery (PoD) 协议

PoD 是实现 zkPoD系统的核心协议。PoD 协议实现了借用区块链智能合约来进行「数据」和 「Token」的原子交换，并且保证买卖双方的公平性。PoD 并没有像 ZKCP[1] 那样采用单一的 zkSNARK 方案来实现原子交换，而是利用了 Pedersen Commitment，Schnorr Protocol 等密码学经典方案。这样 PoD 可以做得更高效，同时易扩展。PoD 协议还将利用形式化的证明来构建坚实的「信任根基」。

本文介绍一个极简的 PoD 协议——PoD-Tiny，这个协议简化了很多细节，并不实用，但是可以帮助读者快速理解 PoD 的原理和面临的挑战。

假设我是卖家，而你需要从我手里买一个数据文件，这个协议的一个大致流程是：

• 步骤一：我把「数据」加密后，传给你
• 步骤二：你把「Token」交给区块链「智能合约」
• 步骤三：我用「密钥」交换「智能合约」手里的「Token」，然后你紧接着可以从智能合约中读取「密钥」进行「数据」解密

  是不是很简单？聪明的你此刻正在高度怀疑这个过程是不是哪有问题。

「公平交易」中的关键问题

• 关键问题(1)：你收到的加密数据确实是你想要的数据
• 关键问题(2)：你收到加密数据之后，不付钱就跑路怎么办
• 关键问题(3)：而我出示给智能合约的密钥必须是真密钥，否则拿不到 Token
• 关键问题(4)：我出示真密钥之后，必须要能拿到 Token

我们接下来就抽丝剥茧，讨论下 PoD-Tiny 是怎么巧妙解决这些问题的。

锁定数据的特征：Authenticator

对于关键问题(1)，我们需要一个锚点，什么是你想要的数据。这里简单起见，假设我们事先约定了一个数据文件的唯一标签，或者特征。然后你购买的数据需要能和这个标签一一对应。

一般来说，大家喜欢用 Hash 来标记对一个字符串的特征，比如计算

h = MD5("hello,zkPoD!")

承诺也叫 Commitment，它可以做到和数据的一一对应，同时并且能够隐藏数据的值。这里的 A 在 zkPoD 系统中被称为「认证信息」 Authenticator。而这里的G 是一个椭圆曲线循环群的生成元。

A = m*G

我们通过下面的运算产生这个数据的「承诺」。

我们看下这个字符串 "hello,zkPoD!" 总共有 12 个字节大小，也就是 96 个 bit。于是我们可以将这 12 个字节转换成一个有限域上的整数（这里我们假设有限域的大小接近 256 bit ）。这样我们可以把这个字符串编码成一个整数，我们姑且用一个符号表示这个整数， 假设是 m。

「认证信息」Authenticator 可以向所有人公开，我们不用担心会泄露原始数据信息。这是因为，通过 A 难以反算出来 m。这个逆运算是一个有限域的「求对数」运算。假如有限域比较大的话，这个对数运算是非常非常困难的，这就是常说的「离散对数难题」假设。抛开这些理论细节，我们只要知道，Authenticator 可以放心交给任何人，而不用担心 m 被逆向破解。

「认证信息」为什么要采用这种「承诺」形式，而不是采用大家所熟知的 Hash 运算。这是因为「承诺」具有加法运算同态性。所谓同态性质，大家可以这么理解：明文数据具有的某种运算，可以同态映射到密文的运算中。假设有三个数据明文，m1，m2 还有 m3，其中 m1 = m2 + m3。

他们的 Authenticator 分别计算如下：

A1 = m1*G， A2 = m2*G， A3 = m3*G，

我们可以计算 A1 ?= A2 + A3

来验证 m1 ?= m2 + m3。大家可以发现，虽然一个吃瓜群众知道了 A1，他也不能反算出m1。但是他仍然知道 m1 等于另外两个数的和，虽然他完全不知道这三个数具体的值是多少。

注：这里的加法是模加，a + b 是 a + b mod p的简写。为了易读性，后续的加减乘除一律约定是有限域上的运算。

剩下的事情就简单了，在 PoD协议中，我们可以任选一个随机数 k 作为一次性密钥，来加密m，计算 E(m) = k + m。 E(m) 就是加密数据。我可以把 K = k*G 也发给你，这样你手里有三样东西，A ，K，还有 E(m)。你就可以用下面的公式来「同态地」校验加了密的 E(m) 确实是数据 m 的密文：

E(m)*G ?= K + A

并且，通过上面的公式，你还能知道一个关键信息：密钥是一个关联到 K 的数值。尽管这时候你完全不知道 m 和 密钥 k。这个信息也是解决关键问题(3)的关键所在。

总结一下：

通过同态性，买家可以在数据加密的情况验证数据是否满足一些条件

回忆一下关键问题(2)：

• 关键问题(2)：你收到加密数据之后，不付钱就跑路怎么办

解决这个问题是核心方法是「零知识证明」。如果买家拿到加密数据之后，从中分析不出来任何多余的信息，那么就不会损害卖家利益，也就能解决关键问题(2)。简单讲，如果加密数据是零知识的，就不怕买家拿了加密数据不给钱就跑路。所谓的「零知识」，大家可以这么通俗理解：买家拿到的加密数据后，就像拿到一堆随机数一样，没有任何信息量。怎么做到零知识呢？PoD-Tiny 采用了经典 Schnorr 协议的思想。

 

插播科普：Schnorr 协议 与 「零知识」

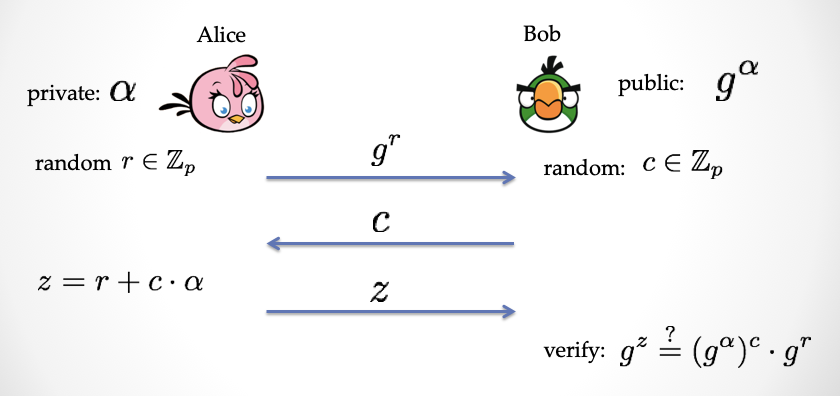
Schnorr 协议是非常经典的教课书例子，我这里快速带大家过一遍。Schnorr 协议的用途之一是用来做身份认证，它是一个两方安全协议，一方「证明者」Alice ，向另一方「验证者」Bob证明她拥有一个公钥对应的私钥。

首先 Alice 产生一对「公私钥」，(PK, sk)。然后 Bob 持有 Alice 的公钥 PK。当 Alice 要向 Bob 证明身份时，他们会通过一个「三步交互协议」来完成证明：证明 Alice 拥有私钥 sk。如果 Bob 接受了这个证明，那么 Bob 会认为 对面证明有私钥的人就是 Alice。下面简单描述下这个协议：

sk = a, pk = a*G

公开输入：PK = a*G

Alice私有输入：sk = a

第一步：Alice 选择一个随机数 r，并且发送 r 的「承诺」R = r*G 给 Bob

第二步：Bob 发回一个随机数 c，作为挑战数

第三步：Alice 计算 z = r + c * a，然后将 z 发送给 Bob，然后 Bob 通过如下的公式来验证：

验证公式：z*G ?= R + c*PK = r*G + c*a*G

这个 Schnorr 协议具有三个性质：

1. 完备性 Completeness
2. 可靠性 Special Soundness
3. 对诚实验证者零知 Special Honest Verifier Zero-Knowledge

其中第三个性质就是「零知识」，这个性质保证了：在协议交互过程中，Bob 无论如何都不会得到关于私钥的任何信息。

注:严格地讲， Schnorr 协议并不是「Full-ZK」，只能保证「HVZK」，这是一个相对弱一些的零知识性质。不过大家暂时不用纠结这一点，Schnorr 协议可以通过一些技巧升级为「Full-ZK」。

PoD-Tiny：一个简单的 PoD 协议

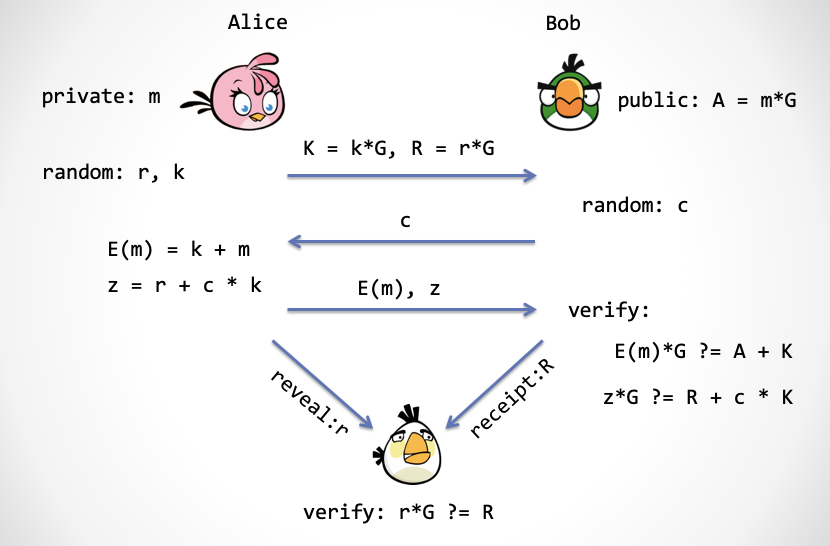
如果大家已经大概记住了 Schnorr 协议的细节，那么我来展示一个协议叫做 PoD-Tiny。

协议描述：假设 Alice 拥有一个数据明文 m，然后 Bob 拥有这个数据的 Authenticator（A），这里还有一个 「Trustless 第三方」，我们暂且叫她 Julia。请大家记住：她是一个智能合约。

协议：

开场前的道具：m,a,G, 一个随机数产生器 rand()

角色：

• Alice：拥有数据 m，一次性密钥 k <-rand()
• Bob：拥有 A
• Julia: N/A

步骤：

第一步：Alice 产生一个随机数，r <-rand() ，然后发给 Bob 两个数 K=k*G 和 R=r*G

第二步：Bob 产生一个随机数 c <-rand()，发送给 Alice

第三步：Alice 计算两个数字 E(m) = k + m，z = r + c * k，并且发送给 Bob。这两个数，第一个 E(m) 是用一次性密钥 k 加密后的「数据密文」，而 z 是「密钥的密文」。

注：什么？密钥的密文？没错，这里 Alice 用第一步生成的随机数 r，加上第二步 Bob 提供的挑战数 c对 k 做了加密，得到了 z。

第四步：Bob 对收到的数据密文 E(m) 进行验证（公式(1) ），并且对密钥的密文进行验证（公式(2) ）：

• 验证公式(1)：E(m) * G ?= A + K
• 验证公式(2)：z*G ?= R + c*K

注：在第四步中，Bob 需要搞明白两件事：首先传给他的密文数据（E(m)）能不能对应到数据锚点（A）；然后密文数据（E(m)）是不是由某一个未知密钥 X 加密的，并且这个「未知密钥」的密文应该等于第三步中 Alice 发过来的「密钥密文」（z）。倘若如此，在未来的某个时刻，若 Bob 得到「密钥密文的密钥」（r） 之后，就可以做两次解密动作来成功拿到数据明文（m）。两次解密动作为：首先 Bob 用「密钥密文的密钥」r 还有挑战数 c 解密 密钥密文 z，得到数据密钥 k，然后再用数据密钥来解密 数据密文 E(m)，从而得到数据明文 m。

再注：上面的协议第一步到第四步，其实大家可以发现和 Schnorr 协议非常类似。只不过把 a 替换成了一个一次性密钥 k。然后另一个不同点是，K = k*G 相当于原 Schnorr 协议中的公钥，并不是一开始发给了Bob，而是在协议的第一步和 R 一起发送给 Bob。不管如何，从整体上，这四步协议正是一个 Schnorr 协议的扩展。当然到这里还没完，接下来区块链要登场了，Bob，Alice 要和 Julia 开始进行交互。

第五步：如果 Bob 在第四步中验证公式(1)和公式(2)通过，那么说明 Alice 发的加密数据都是正确的。这时候 Bob 要发给 Julia 一个「数据交付收据」(Delivery-Receipt)，R。Bob 在这一步需要将 「Token」一并保存给 Julia。

注：这个收据是为了告诉 Julia，Bob 他已经收到了加过密的数据了，但是密钥还没收到。密钥需要 Julia 帮他接收并验证。那么验证的凭据是什么呢？正是「密钥密文的密钥」对应的「承诺」，是不是有点绕，这个收据就是协议第一步 Alice 发给 Bob 的 R。

第六步：Alice 向 Julia 出示「密钥密文的密钥」，也就是 r。Julia 检查下面这个关键公式。如果验证通过，Julia 可以将 Bob 保存的 Token 转给 Alice。

• 验证公式(3)：R ?= r*G

我们看看关键问题(3)是如何解决的。

• 我们看看关键问题(3)是如何解决的。

在协议的第一步，Alice 给 Bob 发送了一个「密钥的密钥」的「承诺」R；然后在协议的第五步，Bob 把 R 转交给了 Julia；第六步，Alice 兑现承诺，揭示对应的 r。如果 Alice 出示一个错误的值，Julia 立即就会发现公示(3)不成立。

还有一个：

• 关键问题(4)：Alice 出示真密钥之后，必须要能拿到 Token

在协议的第六步，Julia 要检验公式(3)。在 Alice 出示正确的 r 的情况下，如果等式不成立，那么只有两种情况：（1）Julia 故意捣乱， （2）R 的值不正确。对于前一种情况，需要保证 Julia 的合约代码确实没有漏洞，功能正常，这个需要额外采用「形式化验证」的方法来解决。对于后一种情况，这里需要 Alice 在第六步先检查一下 Julia 的内部状态，在第五步中 Bob 提交的 R 是不是一个正确的值。这里请注意：Julia 是一个公开的智能合约，她持有的任何数据都是公开可见的，她的任何内部状态与计算过程都是公开可见的。

协议的安全性与公平性分析

如果我们不考虑多次交易，PoD-Tiny 是一个「公平」的交易协议。我们接下来依次分析下为何这个协议是公平的。

我们首先考虑 Alice 有哪些作弊手段：

• A1. 将假的数据 m' 加密后传给 Bob
• A2. 加密数据时用的密钥 k，但是在加密密钥的时候却用的是另一个 k'，并且 k <> k'
• A3. 向 Julia 出示一个假的密文密钥 r'

分析：如果 Alice 采用作弊手法 A1，那么 Bob 在校验公式(1)时能够发现；如果 Alice 采用作弊手法 A2，那么 Bob可以通过计算公式(2)发现；如果 Alice 采用作弊手法 A3，那么 Julia 通过公式(3)能发现。

我们再考虑 Bob 都有哪些作弊手段：

• B1. Bob 在拿到加密数据 E(m) 之后，就退出协议，然后尝试破解密文
• B2. Bob 在验证加密数据之后，向 Julia 出示一个错误的「交付收据」
• B3. Bob 账户没有足够的 Token

分析：如果 Bob 采用作弊手段 B1，那么 Bob 是无法从加密数据中得到任何信息的，因为协议的前三步是「零知识的」（准确地说：Honest Verifier Zero-Knowledge）。如果 Bob 采用手段 B2，Alice 可以在第六步检查下 Julia 手里的「数据交付收据」R 是不是和她在第一步发给 Bob 的相同，一旦 Bob 提交错误的收据，Alice 可以直接退出协议，拒绝出示密钥。同样，如果 Bob 采用手段 B3，Alice 可以在第六步的时候检查 Bob保存在 Julia 处的 Token 是否足够，如果不足则直接退出协议。

最后，Julia 有没有可能作弊呢？Julia 是智能合约，她的任何行为和内部状态都能被任何人读取，那么通过 Julia 是有可能产生信息泄露的，从而对 Alice 或者 Bob 不利。但是请大家注意下，Julia 其实并不接触任何和数据明文 m 相关的信息，也就从链上不会泄露 m 的信息。Julia 接触到的信息只有两个，R 和 r。

压缩到最简协议

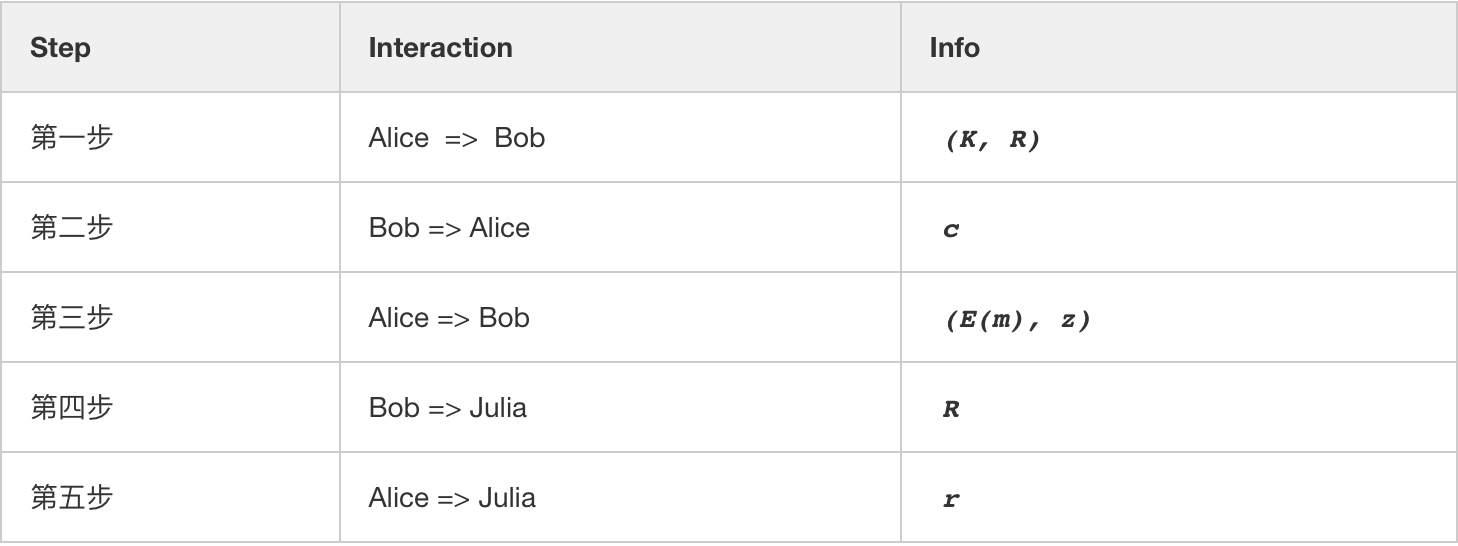
我们数一数上面的协议的交互步骤总共有五步，分别是 Alice 与 Bob交互三次，Bob 与 Julia 交互一次，Alice 与 Julia 交互一次。安全协议里面有一个叫做 Fiat-Shamir Heuristic 变换的工具，它可以将 PoD-Tiny 协议中的前三次交互，直接「压缩」成为一次交互。

压缩前：

压缩后：

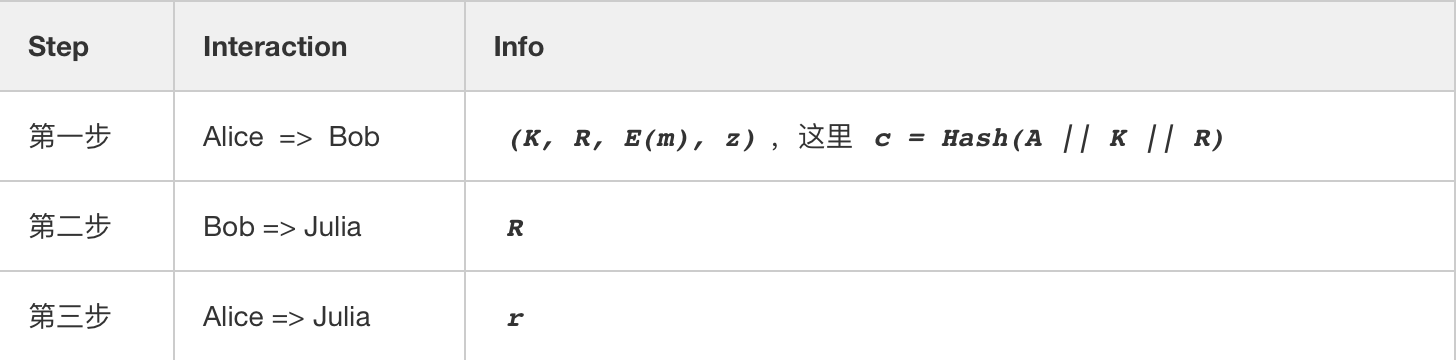
我们发现最主要的不同点是，在压缩后的 PoD-Tiny 中挑战数不再由 Bob 产生，而是由 Alice 产生。这里大家可能会产生疑问，这样做会不会对 Bob 不公平？这相当于三步的 Schnorr 协议直接压缩成一步就完成了。这里先下个结论：压缩后的协议保持零知识的性质，仍然对双方公平。原因是，压缩前的协议可以证明 HVZK(Honest Verifier Zero-Knowledge)；压缩后的协议可以证明出 NIZK (Non-Interactive Zero-Knowledge)。但是安全性在压缩前后的对比会比较 Subtle，这里不再展开。

经过压缩，最后这个协议变得不可思议地简洁：

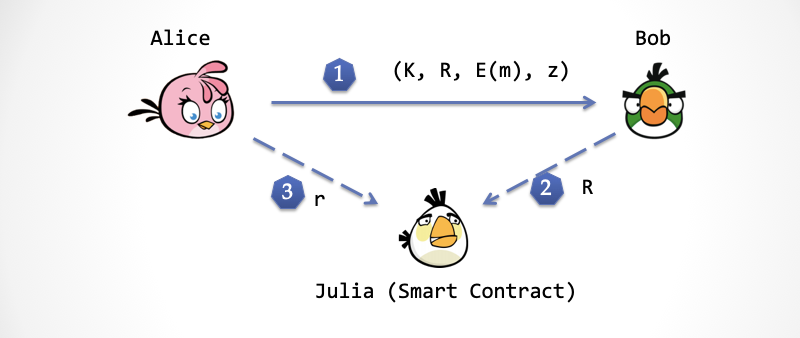
迈向实用性的挑战：安全与性能

最简协议 PoD-Tiny 只是万里长征的第一步，当面对纷繁冗杂的现实世界，要将理论变成代码时，会面临许许多多的问题。这些问题会相互纠缠在一起，反过来又会影响着协议在理论层面的设计。

• 如何支持长度超过 1MB 的数据，甚至上 GB
• 如何有效降低链上验证计算的开销
• 如何支持以太坊，并免疫以太坊上的各式安全问题
• 如何支持数据的复杂同态计算

在安全和性能方面，zkPoD 做了不少的工程改进和创新，感兴趣的朋友请关注我们的后续文章。

写在最后

区块链到底能做什么？我在最近一年里看到了许多相当「悲观」的论调，我想 PoD 协议应该会给这些怀疑论者带来些许启发。区块链在 PoD 协议中起到了一个「Trustless 第三方」的关键角色，并且让这个协议变得不可思议的简洁，这是我们始料未及。

参考文献

• [1] Maxwell, G. "Zero knowledge contingent payment. 2011." URl: https://en.bitcoin.it/wiki/Zero_Knowledge_Contingent_Payment (visited on 05/01/2016) (2016).
• [2] Greg Maxwell. “The first successful Zero-Knowledge Contingent Payment.” https://bitcoincore.org/en/2016/02/26/zero-knowledge-contingent-payments-announcement/

本文作者：郭宇