摘要 区块链技术是比特币平台的底层技术，由于其具有透明性、不可伪造性、不可更改性等特点，被广泛应用于虚拟货币、供应链等系统中.然而，大部分区块链平台，如比特币平台，面临包括自私挖矿在内的诸多问题，这将直接导致比特币并不安全，从而严重影响区块链的发展.自私挖矿是一种比特币挖掘策略，它是指自私矿工选择性地发布之前的隐匿的区块从而获得比诚实矿工更多的额外收益.本文在模拟诚实矿工挖矿实验基础上，重点研究自私挖矿情况下矿工的最佳相对收益.采用中心极限定理和节点状态转化图建立了两个节点分布概率模型，再运用马尔可夫随机过程和函数极值法依次求得两个模型下的最佳收益.同时设计并进行自私挖矿模拟实验，得出自私挖矿中节点算力和收益的关系，从而进一步验证模型的合理性.

0 引言

21世纪以来，互联网技术的蓬勃发展极大地改善了人民群众的日常生活，这使得互联网成为信息社会不可或缺的重要保障，但与此同时，互联网也面临各种安全问题，比如黑客攻击、数据泄露等.区块链技术作为一种分布式数据存储、点对点传输、共识机制、加密算法和智能合约等计算机技术应用新模式，具有去中心化、透明性、不可更改性等特点，因此，它在金融、电子政务、能源应用和医疗等诸多领域发挥着重要作用[1].

比特币系统的稳定性依赖于参与交易的节点的共同利益.在诚实节点发现新的区块时，会立即向整个系统公布挖掘到新区块的消息.在接收和确认该消息后，其他矿工会将这笔交易记录在账本上，然后开始挖掘其他分支.率先挖到区块的矿工会得到相应的奖励.这种激励机制让比特币在去中心化的情况下，依然能使交易各方达成共识，从而很好地维护了区块链系统的稳定性.然而，当前的比特币系统中，恶意节点为了获得更大的收益，往往会采用自私挖矿的策略[2].自私挖礦的概念是由康奈尔大学两位研究员Eyal和Sirer于2013年提出的，它是一种比特币的挖掘策略，是一种基于挖矿节点算力的竞争[2].恶意节点依据“自私矿池”中区块的私密性，当一个“自私矿池”挖到新的区块，并没有根据比特币共识协议立即公布该区块，从而让其余的诚实节点浪费算力去挖矿[3].面对区块链出现分叉的情况，最长的那一条链被视作合法链[4-5].当诚实链的长度即将接近自私链的长度时，自私矿工就会释放之前隐藏的区块从而迫使诚实矿工的劳动作废.在自私挖矿的情况下，自私矿工可以获得相对于其采用诚实挖矿策略较多收益，而诚实矿工则会损失自己的合法收益.除此以外，来自康奈尔大学和马里兰大学的区块链研究员Nayak等[6]更进一步提出对于大型参数空间而言，自私挖矿并非最佳选择.因而他们拓展了采矿战略空间，考虑一类顽固的采矿策略，即攻击者继续在他的私人分支上进行挖矿，让公共分支领先，如果他以后碰巧超越公众，他将获得比期望更高的挖矿收益[7].这种情况下，计算表明袭击者的收益最大会提高13%.此外，其他一些研究展示了如何通过非平凡的挖掘组合和网络攻击进一步放大他的收益，从而获得更大的挖矿收益，例如，分布式去中心化的Eclipse攻击的策略[4].

虽然，目前针对比特币挖矿策略的研究有很多，不同的研究工作研究了自私旷工从不同的角度来进行自私挖矿，从而获得额外的收益.但是，这些研究都没有从一个系统的角度来分析和总结比特币节点可能的挖矿策略.本文将针对现有的比特币平台中挖矿模型进行系统总结，并通过数学模型来定量分析这些自私挖矿策略获取的收益.最后，本文将给出一些可能的策略以防止自私挖矿，希望能为初学研究者提供一个系统、全面地了解比特币的挖矿模型，同时为比特币挖矿策略优化提供一些可行的建议.

1 自私挖矿模型和收益模型

1.1 比特币简介

比特币作为一种加密数字货币，其本质是包含一系列输入输出列表的数据结构，包含了节点与节点之间的转账记录.比特币交易和挖矿过程包含6个步骤，如图1所示[8].

1）某客户向P2P网络发出交易请求;

2）接收到用户请求的节点验证交易信息，将其向P2P网络进行广播;

3）各矿工接收到交易信息，验证其正确后将其放入交易池，并继续广播该交易信息，直到全网都接收到该笔交易信息;

4）将多条交易信息打包成一个新的区块;

5）将新的区块加入到已经存在的区块链中;

6）客户的交易完成.

比特币的有效性建立在交易发起者的签名上，交易签名的作用是为了防止他人冒充签名，产生数据造假.交易输入的签名是指放在交易输入中的签名（Signature）字段，其中包括了用户的公共秘钥（Pubkey）.签名字段主要用于之后的交易有效性验证.

交易完成后，系统会把交易广播给邻居.挖矿节点，俗称矿工，在挖矿时，会把交易池中的交易记录打包形成一个新的区块.在成功加入区块链交易系统以后，这笔交易就会被系统确认，但是在挖矿节点进行交易之前，需要验证交易真伪，防止数据造假[9].

1.2 自私挖矿模型

自私矿工通过隐匿和公布私有区块从而获得额外收益，但关键问题在于自私矿工何时选择公布自己隐匿的区块或者何时继续隐藏挖掘到的新区块才能使得自己的相对收益达到最大.

本文采用〈S，A，P，R〉模型[10]，将自私挖矿问题转化为决策问题，目标函数是相对收益函数.需要阐明的是此处的目标函数是非线性的，因为自私挖矿者所追求的并不是所获区块的具体数量，而是使自己所获得的区块的份额最大化.换而言之，自私挖矿者想得到的是相对其他挖矿节点更高的投资回报率.其中，S代表区块状态集中的某种状态.可以用三元式（la，lh，fork）表示S的空间状态.其中前两个参数分别表示自私矿链的长度和诚实矿链的长度，第三个参数表示区块链的分叉.A为行动集，该行动集中有4种元素：接受、发布、隐匿和竞争.P表示在某种行动下，当前区块的状态转化到下一状态的概率.R表示当前状态下的期望收益.

1.2.1 节点分布概率分析

本文从节点分布概率的角度出发，建立2个自私挖矿过程模型.第1个模型直接利用泊松分布和大数定律来拟合诚实节点和自私挖矿节点的概率分布.第2个模型基于状态转换图中的转换频率来分析矿池中的节点概率分布.需要指明的是，在2个模型建立与分析过程中，都忽略区块大小、网络通信延迟等因素.

1）模型1：概率分析

① 诚实节点概率分布

诚实节点的概率分布近似于泊松分布[11].一般而言，比特币每600 s挖掘出一个新块，由文献[12]可知，一个诚实节点挖到块的概率为Ph.

其中，1-α指诚实矿工的算力，d是挖矿难度，t是挖矿的时间（以s为单位）.

② 自私节点概率分布

由于自私挖矿池中节点的算力基本稳定，所以本文假定自私节点发掘一个新区块的概率基本不变.

考虑到随着自私挖矿的深入，不断会有诚实节点加入到自私挖矿的行列中来，这就导致了自私矿池的算力发生变化.所以，用p′表示自私矿池变化后的概率分布.

2） 模型2：概率分析

模型2将矿池中的节点的状态进行分类.为了直观表示，本文将节点状态标注为0′，0，1等.节点状态转化如图2所示[2].其中状态0代表只有一条公共链，0′表示有两条长度为1的链，其中一条是主分支，另外一条是自私挖矿者的私有分支，用以发布隐匿区块从而和主分支竞争[2].另外，本文中用β来表示矿池中诚实节点的比例.

在频率为α（本文将算力α等价为转换频率），对于状态S=0，1，2，…，节点在挖掘出新的区块后状态会从S变为S+1.对于状态S=2，3，4，…，在频率为1-α的情况下，状态会从S退回S-1.如果自私矿池中有一个长度为1的自私挖矿链，而在其他分支上挖掘到一个新区块的同时自私矿链采取公布隐藏区块的措施，这样系统就会产生故意分叉现象，即出现两个长度为1的区块链.自私矿池中的矿工会继续挖掘该矿池上的分支，而诚实矿工则依然在他们之前认定的矿链上继续挖矿.

通过图2可以得知，从状态0′出发有3种可能的转换，最终全部通向状态0.它们的总频率之和为1.第1种情况，矿池以频率α在之前的自私链上挖掘到一个新区块;第2种情况，其他矿工在之前的自私链上以频率β（1-α）挖掘新的区块;第3种情况，其他矿工在公共链上以频率（1-β）（1-α）挖掘到新的区块.

由状态转化图可以推导出节点状态概率分布，结论如式（1）：

1.2.2 相对收益分析

目标函数是节点相对收益函数，因为自私挖矿者所想的是最大化所获得的区块份额，而不是获得区块的具体数量.换而言之，自私挖矿者想得到的是相对其他挖矿节点更高的投资回报率.

1）模型1：相对收益分析

結合自私挖矿过程分析和挖矿节点概率分布，对于何时公布隐匿区块的关键问题，给出以下算法描述（算法1）.

根据算法1，建立自私挖矿节点的相对收益函数[13]，如式（5）所示：

最后一步是要确定取得最优解时ρ的值.由于ρ∈（0，1），所以可以采用二分查找的方法来确定ρ的最优值，二分查找法伪代码表述如算法2.

2） 模型2：收益分析

结合节点状态转化图2，利用节点状态转化频率来分析自私挖矿的预期收入.目标函数是相对收益函数，如式（7）所示：

下面根据自私链和诚实链的不同状态来讨论相对收益.

情况1.系统产生长度均为1的自私链和诚实链的分叉，自私链发现一个新的区块并将它链接到自私链上隐藏.这样，自私链就领先诚实链1个区块的长度，收益也由此决定，如图3所示.

情况2.区块链产生两个分支长度均为1的分叉，此时，自私链发现一个新的区块.自私矿池选择发布自私链上的所有区块.因此，诚实链上的所有区块收益无效，自私链获得两个区块的收益，如图4所示.

情况3.区块链产生两个分支长度均为1的分叉.当诚实链先挖到区块，并将新挖到的区块链接到自己的诚实链上.自私挖矿链会采取接收行动，即放弃自私链上所有的区块.这种情况下，诚实链获得两个区块的收益，如图5所示.

情况4.区块链产生两个分支长度均为1的分叉.如果诚实链挖矿到一个区块，诚实链可以采取一种策略，即将新挖到的区块链接到自私链的后面，这样自私链和诚实链先各自获得一个区块的收益.然后，自私挖矿链后续的收益就会被诚实挖矿链所有，如图6所示.

情况5.没有自私分支，若诚实链发掘一个新区块，则诚实链获得一个区块的收益.此时，诚实链的相对收益为p0（1-α）.

情况6.在自私链领先诚实链一个区块的情况下，诚实链率先挖掘到一个区块.此时，两者的长度一样，此时利益归属取决于两者之间的算力博弈的结果.

情况7.当自私链领先诚实链两个区块的情况下，如果诚实链挖到1个新区块，则la-lh≥1，自私链会采取发布措施，从而迫使诚实链上的收益全部作废，两个区块的收益归属自私链.

情况8.自私链领先诚实链的长度超过2块，此时，诚实链缩短两者差距至2个区块.自私链会选择发布它的分支上的某一个区块.这种情况下，诚实链挖到的新区块没有链接到诚实链上，而是链接到其他主链上了.这样诚实链上的区块收益都作废，自私挖矿链可以盈利一个区块的收益，如图8所示.

接下来将根据上述8种情况分别计算诚实链的收益和自私链的收益.其中，情况3，4，5的收益为诚实链所有，情况1，2，6，7，8的收益为自私链所有.然后，再依据状态转化图可得到自私节点和诚实节点各自的相对收益，双方各自的相对收益如式（8）所示.

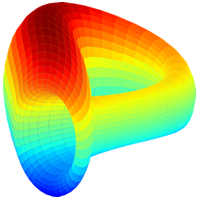
规定好α，β的范围，将求R的最优解转化为定义域内求二元函数的极值问题.同时，利用MATLAB做出相对收益函数R的图像，如图9所示.

由表达式（9）可以看出，相对收益函数是由α，β共同决定的，所以将最佳收益问题转化为在α，β的可行域内求函数极值.根据文献[15]，利用相关挖矿系数，可以发现当β为0时，α的阈值为1/3，即自私矿工只要掌握全网1/3的算力就可以保证获得额外收益，这符合我们之前的认知.当β的值为0.5时，α的阈值为1/4，即当自私节点占据总节点数的一半时，自私矿工只要拥有全网1/4的算力就可以获得比诚实矿工更多的额外收益.

2 挖矿实验模拟

2.1 诚实挖矿模拟实验结果与分析

2.1.1 实验环境

模拟系统采用Go语言实现，基于以下软、硬件环境开发模拟系统并进行实验数据的收集与处理.

硬件环境：Intel（R） Core（TM） i5-8300 CPU @ 2.30GHz，8G内存.

软件环境：Ubuntu 18.04，LiteIDE X35.5，go 1.11.1.

实验过程中以Linux系统的终端来模拟各个节点，节点间通过广播信息进行信息交互，产生的实验结果采用Excel和MATLAB进行分析.

2.1.2 诚实挖矿实验内容设计

为简化实验，假设一条记录为一个区块，矿工挖矿成功的收益为1，且交易费用为0.本文针对诚实矿工挖矿设计了一个实验，对具有不同算力的10个矿工进行了2 000次模拟交易，统计各个节点的收益，并对数据进行了分析，得出节点的算力和收益之间的关系.

2.1.3 实验结果分析

为方便计算，事先设置好总的算力值为80 000，其中矿工M1至M10各自所占总算力的比例为：6%，7%，7.5%，8.5%，9.5%，10.5%，11%，12%，13% 和15%.

经过2 000笔交易以后，各矿工的最终收益如表1所示.

实验中不同算力下的10个诚实挖矿节点的理论收益率与实际收益率对比如表2所示.实验数据表明理论收益与实际收益的误差率在合理范围内.

从表1可知，2 000笔交易中丢失了两笔交易记录.同时，表2显示各个矿工的算力所占百分比和节点收益百分比基本持平，即节点拥有多少挖矿算力就几乎可以获得多少收益.对于一个诚实节点而言，其拥有的挖矿算力越大所获得的收益就越多.

2.2 自私挖矿模拟实验结果与分析

2.2.1 实验环境

自私挖矿模拟实验的实验环境和诚实挖矿实验表2 各矿工理论收益与实际收益对比环境相似，此处不再赘述.

2.2.2 自私挖矿实验内容设计

本次自私挖矿实验共建立4个挖矿节点，1个发送节点和1个统计节点（即在Linux系统中建立4个挖矿终端节点，1个发送终端，1个统计终端）.在本实验中，我們设置用每分钟计算哈希值的个数来表示算力，4个挖矿节点分为2个算力分别为15 000（占总体算力的18.2%）和27 500的自私节点（占总体算力的33.3%），以及2个算力均为20 000（占总体算力的24.2%）的诚实节点.实验共进行1 000次模拟挖矿实验，统计各个挖矿节点的收益.

2.2.3 自私挖矿模拟实验结果与分析

自私挖矿模拟实验的结果如表3和表4所示.其中，SM1和SM2分别表示算力为15 000和27 500的自私挖矿节点，M11和M12别表示另外2个相同算力的诚实挖矿节点.

由表3，表4可以得知，两个自私挖矿节点同时进行自私挖矿的情况下，整个系统交易丢失率整体上趋于平稳，丢失率基本稳定在30%左右.两个自私挖矿节点由于算力的不同，存在收益上的差异.自私挖矿节点SM1的算力占系统总算力的18.18%，收益却只有总收益的13.68%;而自私挖矿节点SM2的算力占系统总算力的1/3，收益却达总收益的37.85%.由此可见，SM1和SM2之间存在以算力为主要因素，其他多因素共同作用的博弈过程，同时SM1的算力也低于其余两个诚实节点.

上述实验数据表明，在自私挖矿过程中，如果节点的算力过小，将很难获得额外的收益，甚至会少于其采用诚实挖矿策略的收益.当自私节点的挖矿算力达到整个系统算力的1/3时，自私节点可以获得比诚实挖矿策略更多的额外收益.

3 总结

本文研究了比特币平台中的比特币挖掘策略，系统地展示了不同挖矿策略下旷工的收益情况.首先简要介绍了自私挖矿的概念和比特币的原理，然后利用大数定律和矿池中节点状态转化图建立了两个自私挖矿模型.分别采用马尔可夫随机过程和函数极值法求得各模型下的最佳相对收益，最后实验验证自私挖矿与算力之间的关系.

参考文献References

[1] 邹均，于斌，庄鹏，等.区块链核心技术与应用[M].北京：机械工业出版社，2018

ZHOU Jun，YU Bin，ZHUANG Peng，et al.Blockchain core technology and application[M].Beijing：Machine Press，2018

[2] Eyal I，Sirer E G.Majority is not enough：bitcoin mining is vulnerable[J].Communications of the ACM，2013，61（7）：95-102

[3] 袁勇，王飞跃.区块链技术发展现状与展望[J].自动化学报，2016，42（4）：481-494

YUAN Yong，WANG Feiyue.Blockchain：the state of the art and future trends[J].Acta Automatica Sinica，2016，42（4）：481-494

[4] Heilman E，Kendler A，Zohar A，et al.Eclipse attacks on Bitcoin's peer-to-peer network[C]∥Usenix Conference on Security Symposium.USENIX Association，2015：129-144

[5] 夏清，张凤军，左春.加密数字货币系统共识机制综述[J].计算机系统应用，2017，26（4）：1-8

XIA Qing，ZHANG Fengjun，ZUO Chun.Review for consensus mechanism of cryptocurrency system[J].Computer Systems & Applications，2017，26（4）：1-8

[6] Nayak K，Kumar S，Miller A，et al.Stubborn mining：generalizing selfish mining and combining with an eclipse attack[C]∥2016 IEEE European Symposium on Security and Privacy （EuroS&P）.IEEE，2016

[7] Eyal I.The miner's dilemma[C]∥2015 IEEE Symposium on Security and Privacy.IEEE，2015：89-103

[8] Anish L J.Bitcoin and other cryptocurrencies-all you need to know[EB/OL].[2017-06-02].https：∥www.insurancefunda.in/Bitcoin-cryptocurrency/

[9] 李旭東，牛玉坤，魏凌波，等.比特币隐私保护综述[J].密码学报，2019，6（2）：133-149

LI Xudong，NIU Yukun，WEI Lingbo，et al.Overview on privacy protection in bitcoin[J].Journal of Cryptologic Research，2019，6（2）：133-149

[10] 高永琳，程晓荣.区块链中的自私挖掘研究与分析[J].计算机工程与应用，2018，54（15）：62-66

GAO Yonglin，CHENG Xiaorong.Research and analysis of selfish mining for blockchain[J].Computer Engineering and Applications，2018，54（15）：62-66

[11] Nakamoto S.Bitcoin：a peer-to-peer electronic cash system[EB/OL].（2017-02-03）[2019-08-08].https：∥bitcoin.org/bitcoin.pdf

[12] Heilman E.One weird trick to stop selfish miners：fresh bitcoins，a solution for the honest miner[C]∥International Conference on Financial Cryptography and Data Security.Springer，Berlin：Heidelberg，2014：161-162

[13] Gervais A，Karame G O，Wüst K，et al.On the security and performance of proof of work blockchains[C]∥Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security.ACM，2016：3-16

[14] Sapirshtein A，Sompolinsky Y，Zohar A.Optimal selfish mining strategies in bitcoin[M]∥Financial Cryptography and Data Security.Berlin，Heidelberg：Springer Berlin Heidelberg，2017：515-532.DOI：10.1007/978-3-662-54970-4_30

[15] Swanson E.Bitcoin mining calculator[EB/OL].（2017-02-03）[2019-08-08].http：∥www.alloscomp.Com/bitcoin/calculator