Plasma Cash推出的最重要的改进之一是“light proofs”。Plasma 结构要求用户下载整个Plasma 链，以确保他们的资金安全。使用Plasma Cash，他们只需下载与自己资金相关的Merkle树枝。

这是通过引入一个新的事务有效性条件来实现的：特定CoinID的事务只在Merkle树的CoinIdth叶中有效。因此，只下载该分支就足够确信该硬币不存在有效的交易。这个方案的问题在于，交易是“卡”在这个面额上的：如果你想交易多个硬币，你需要多个交易。

如果我们将基于范围的事务放入常规Merkle树的分支中，则light proofs就变得不安全。这是因为有一个分支并不能保证其他分支不相交：

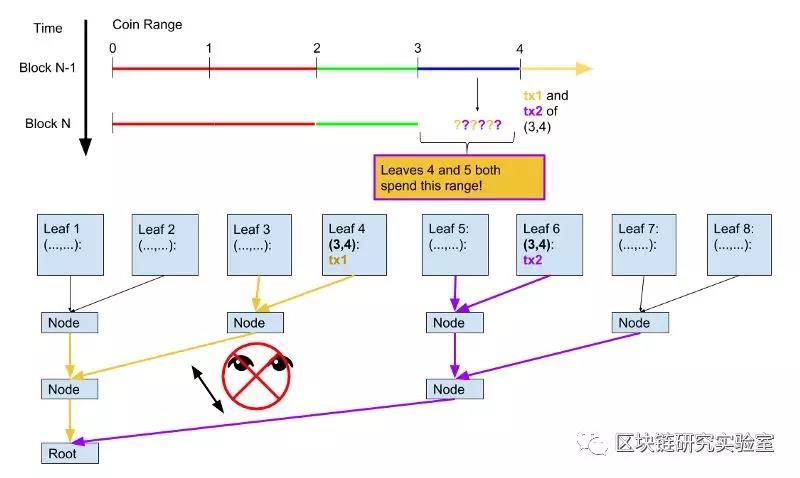
第4和第6叶都描述了范围内的交易（3,4）。有一个分支并不保证另一个分支不存在。

使用常规Merkle树，保证没有其他分支相交的唯一方法是将它们全部下载并检查。但那已经不再是light proofs！

我们的Plasma实现的核心是一个新的块结构，以及一个伴随的新事务有效性条件，它允许我们为基于范围的事务获得light proofs。块结构称为Merkle sum树，其中每个散列旁边是和值。

新的有效性条件使用特定分支的和值来计算开始和结束范围。这种计算是经过精心设计的，因此两个分支的计算范围不可能重叠。转移只有在其自身范围在该范围内时才有效，因此这将使我们返回我们的轻客户！

本节将详细说明sum tree的规范、范围计算的内容以及如何实际构造满足范围的sum tree。

我们已经编写了Plasma-Merkle sum tree的两个实现方法：一个是在操作员的数据库中完成，另一个是在内存中用于在Plasma实用程序中测试。

sum tree 节点规范

Merkle sum树中的每个节点都是48个字节，如下所示：

[32 byte hash][16 byte sum]

总和的16字节长度与coinID相同并不是巧合！

我们有两个辅助属性，.hash和.sum，这两个属性将引出这两个部分。

例如，对于somenode = 0x1b2e79791f28c27ed669f257397e1deb3e522cf1f27024c161b619d276a25315ffffffffffffffffffffffffffffffffff

我们有node.hash == 0x1b2e79791f28c27ed669f257397e1deb3e522cf1f27024c161b619d276a25315和node.sum == 0xffffffffffffffffffffffffffffffffff。

父级计算

在一个规则的merkle树中，我们构造一个哈希节点的二叉树，直到一个根节点。指定和树格式是一个简单的问题，即定义父（左，右）计算函数，该函数接受两个兄弟作为参数。

例如，常规Merkle sum树具有：parent = function（left，right）{return Sha3（left.concat（right））}其中Sha3是哈希函数，concat将这两个值附加在一起。

若要创建merkle sum tree，父函数还必须连接其子函数的加法运算结果。sum值：

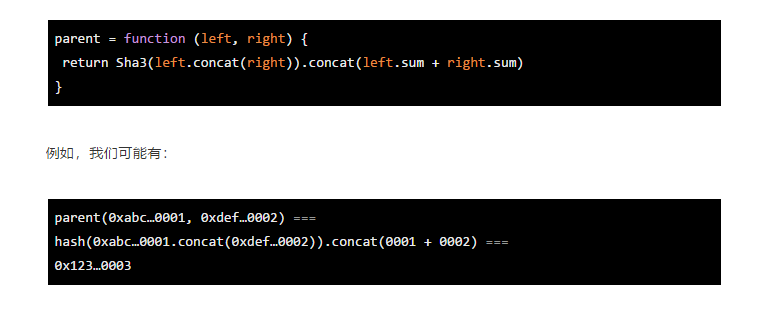
注意parent.hash对每个sibling.sum和hashes是一种承诺：我们对两者的完整96个字节进行哈希处理。

计算分支的范围

我们使用Merkle sum tree的原因是因为它允许我们计算分支描述的特定范围，并且100％确信不存在其他有效的重叠分支。

我们通过在分支上加上左和右和来计算这个范围。在每个父级计算中，将两者初始化为0。如果包含证明指定了右侧的同级，则取right sum+=right.sum；如果将left sum+=left.sum添加到左侧，则取left sum+=left.sum。

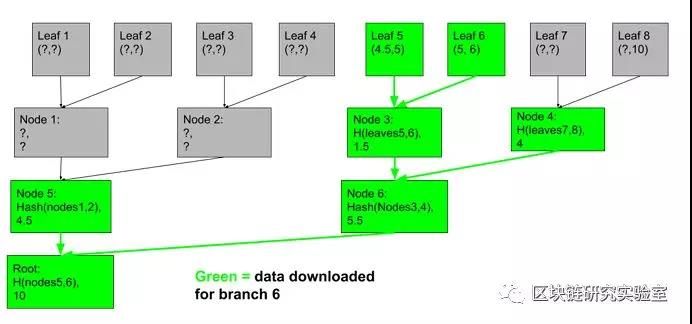
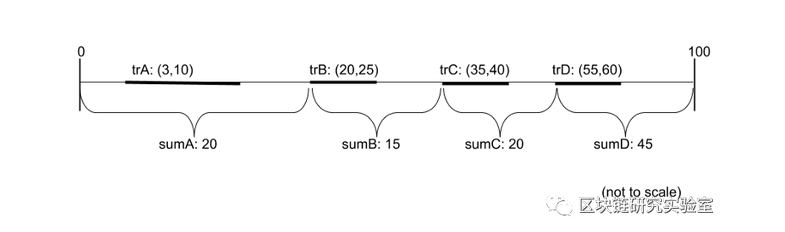
然后，分支描述的范围是[leftsum，root.sum-rightsum]。请参见以下示例：

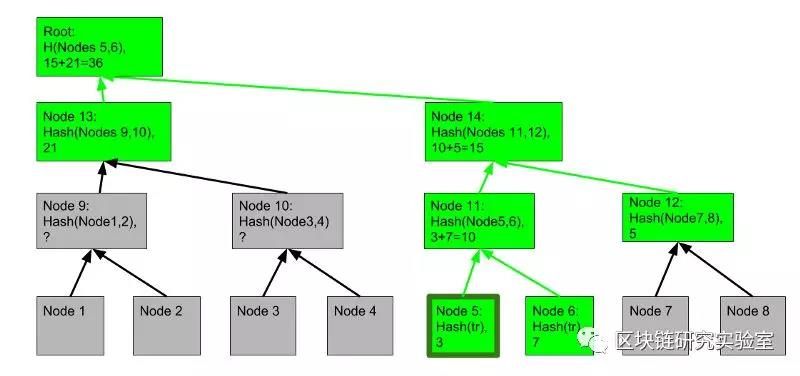
在本例中，分支6的有效范围是[21+3，36–5）==[24，31]。注意31–24=7，这是叶6的总和值！同样，分支5的有效范围是[21，36-（7+5））==[21，24）。注意它的结束和分支6的开始是一样的！

你会发现构造一个Merkle sum tree是不可能的，它有两个不同的分支覆盖相同的范围。在树的某个层面，总和必须被打破！尝试通过制作另一个与范围（4.5,6）相交的分支来“欺骗”叶子5或6。仅填写灰色框中的？

你会发现，在树的某个层次上，这是不可能的：

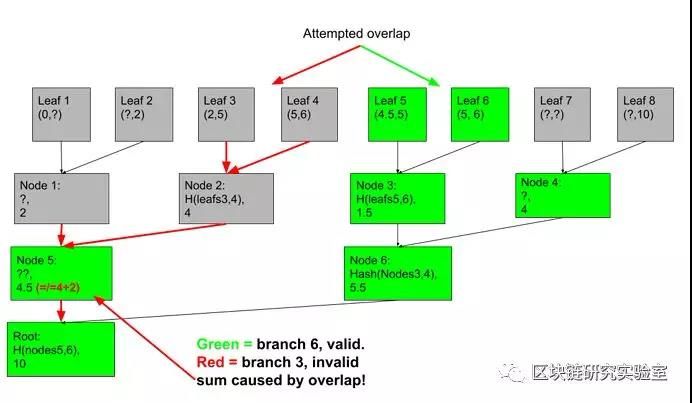
这就是我们获得轻客户的方式。我们将分支范围称为implicitStart和implicitEnd，因为它们是从包含证明中“隐式地”计算的。我们在plasma-utils中通过calculateRootAndBounds（）实现了一个分支检查器，用于测试和客户端证明检查：

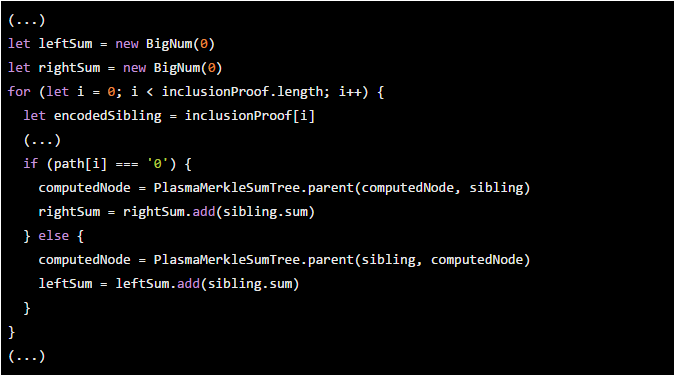
在Vyper中使用智能合约

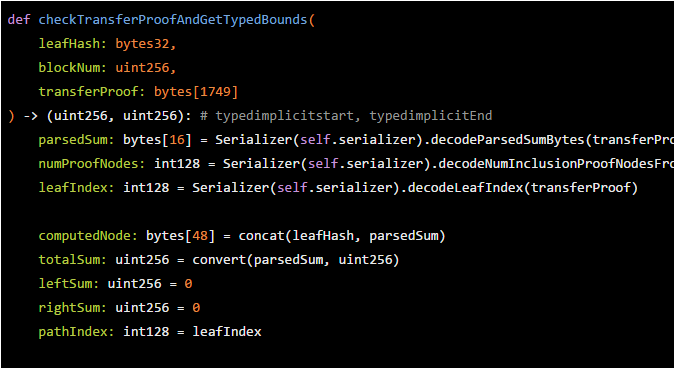
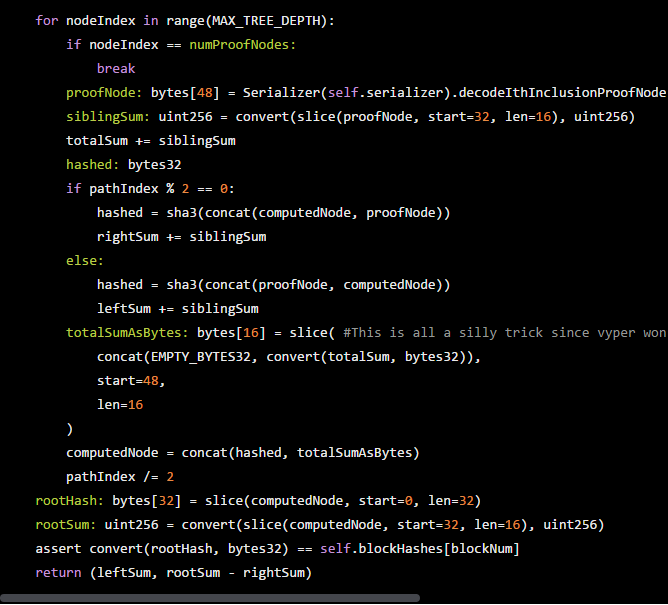
请注意，键入的范围是开始和结束，即完整的16个字节。

在常规Merkle树中，我们通过散列“叶子”构建底层节点：

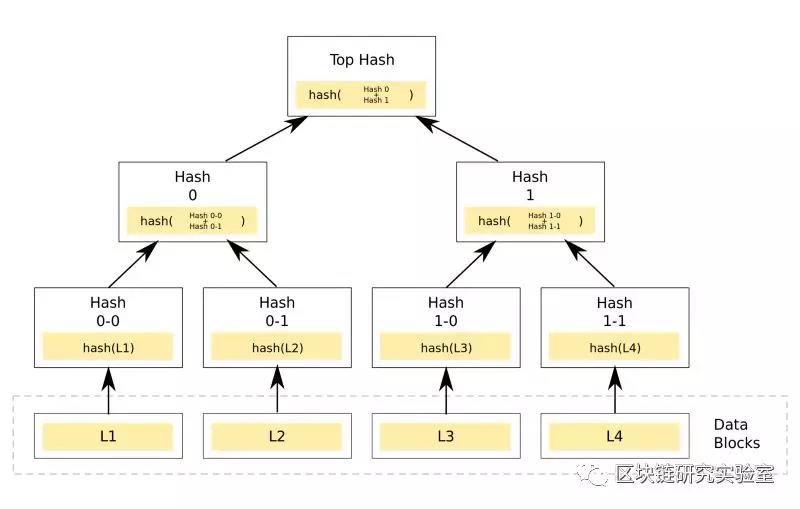
给定一个带有单个transfera的txa，和值应该是什么？事实证明，不仅仅是transfera.end-transfera.start。原因是，如果传输不接触，它会破坏分支的范围。我们需要“填充”sum值来解释这个间隙，否则root.sum将太小。

有趣的是，这是一个非确定性的选择，因为您可以将节点填充到间隙的右侧或左侧。 我们选择了以下“左对齐”方案来将叶子解析为块：

我们将最底层的.sum值称为该分支的parsedSum，而TransferProof模式包含一个.parsedSum值，用于重建底部节点。

分支有效性和隐含NoTx

因此，由智能合约检查的分支的有效性条件如下：implicitStart <= transfer.typedStart <transfer.typedEnd <= implicitEnd。注意，在“Plasma CashFlow”中的和树的原始设计中，一些叶子被填充了一个特殊的“notx”事务，以表示范围没有被处理。使用这种格式，不进行交易的钱币仅为[implicitstart，transfer.typedstart]和[transfer.typednd，implicitend]范围内的钱币。智能合约保证这些范围内的硬币不能用于任何挑战或对退出的反应。

原子性多发（Atomic Multisends）

通常（为了支持交易费用和交换）交易要求多次转移要么发生或要么不发生，结果是每个.transfer需要包含一次有效的事务 - 每个.transfer都有一个与特定transfer.typedStart和.typedEnd相关的有效总和。但是，对于这些包含中的每一个，它仍然是完整的UnsignedTransaction的哈希 - 而不是被解析到底部的单个Transfer.hash。

本文转载公众号：区块链研究实验室

海纳学院的内容将围绕：区块链技术，产品社群，经济模型等全方位的知识体系输出。欢迎联系作者微信：csschan1120